15. Modelling proportion data using the binomial distribution#

本节需要的包：

require(s20x)
Hide code cell output 
Loading required package: s20x

15.1. Binary (Bernoulli) data, odds and log-odds#

Here we are considering the situation where the response can only take two possible values. These might be coded in the form of:

  • Zeros or ones.

  • TRUE or FALSE.

  • Yes or No.

  • Success or Failure.

  • Or any other pair of categorical values.

Bernoulli random variables(伯努利随机变量):

If Y is a Bernoulli random variable with parameter p, then Y will take the value 1 with probability p, and the value 0 with probability 1 - p. Since it is a probability, p must be a value that is between 0 and 1, i.e. \(p ∈ [0, 1]\).

很容易表明，伯努利随机变量的平均值为：

\[ E(Y) = p \]

而且，方差为

\[ Var(Y) = p(1 - p) \]

15.1.1. Odds#

为了使 glm 对数几率的解释更加容易，我们需要引入 Odds 这个概念，把定义域从 \([0, 1]\) 扩展到 \([0, \infty]\)。

Odds 是指事件发生的概率与事件不发生的概率的比值，即：

\[ Odds = \frac{p}{1 - p} \]

反过来说：

\[ p = \frac{Odds}{1 + Odds} \]

15.1.2. Log-odds#

Odds 的对数（简称为 log-odds）为：

\[ LogOdds = log(\frac{p}{1 - p}) \]

此时定义域从 \([0, \infty]\) 变为 \([-\infty, \infty]\)。

\[ p = \frac{exp(LogOdds)}{1 + exp(LogOdds)} \]

15.2. Modelling log-odds#

Why log-odds?

由于我们的模型对或的值没有限制，所以在设置变量为 \(β_0\)、\(β_1\) 的情况下，\(β_0 + β_1 x\) 可以在实线上取任何值。

That is, \(\beta_0+\beta_1x\in(-\infty,\infty)\).

\[ \text{Log-Odds}=\beta_0+\beta_1x \]

Log-Odds can be any real number.

即：

\[ \text{log}\left(\frac{p}{1-p}\right)=\beta_0+\beta_1x \]

其中p是解释变量x的主体 "成功" 的概率。

This can be re-arranged in the logistic form

\[ p=\frac{exp(\beta_0+\beta_1x)}{1+exp(\beta_0+\beta_1x)} \]

15.3. Modelling the response when it is binary (ungrouped data) via glm#

bb.df <- read.csv("../data/basketball.csv")
head(bb.df, 10)
A data.frame: 10 × 3
distancegenderbasket
<int><chr><int>
13M1
21F1
32M1
43M0
51M1
62F1
72F1
81F1
93F0
101F1
 
success.tbl <- xtabs(basket ~ distance + gender, data = bb.df)
success.tbl

        gender
distance  F  M
       1 10 10
       2  6  5
       3  2  1

bb.fit <- glm(
    basket ~ distance * gender,
    family = binomial, # binomial distribution
    data = bb.df
)

plot(bb.fit, which = 1, lty = 2)
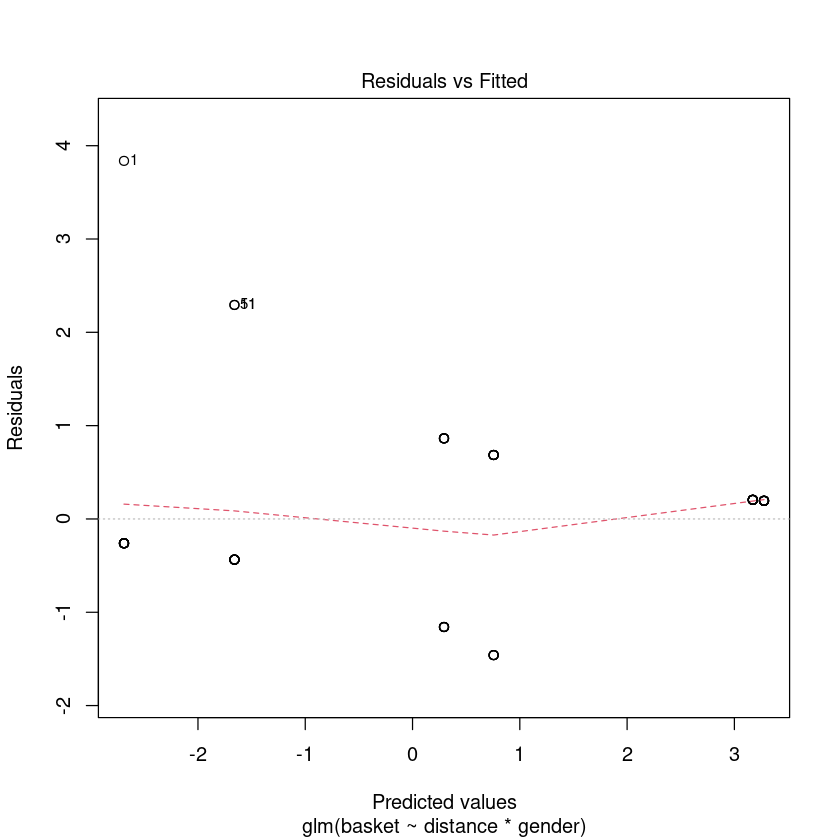
_images/3000ac95c5dacb93009c77d2c05930614790a70bf02bdc2bd15480cf1f92babc.png 
summary(bb.fit)

Call:
glm(formula = basket ~ distance * gender, family = binomial, 
    data = bb.df)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5106  -0.5900   0.2723   0.2866   2.3474  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)   
(Intercept)        5.5878     1.9050   2.933  0.00335 **
distance          -2.4159     0.8181  -2.953  0.00314 **
genderM            0.6710     2.9235   0.230  0.81847   
distance:genderM  -0.5668     1.3213  -0.429  0.66794   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 82.108  on 59  degrees of freedom
Residual deviance: 46.202  on 56  degrees of freedom
AIC: 54.202

Number of Fisher Scoring iterations: 5

bb.fit1 <- glm(basket ~ distance + gender,
    family = binomial, data = bb.df
)
summary(bb.fit1)

Call:
glm(formula = basket ~ distance + gender, family = binomial, 
    data = bb.df)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5382  -0.5411   0.2461   0.3219   2.2283  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   6.1469     1.5242   4.033 5.51e-05 ***
distance     -2.6648     0.6364  -4.188 2.82e-05 ***
genderM      -0.5478     0.7486  -0.732    0.464    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 82.108  on 59  degrees of freedom
Residual deviance: 46.392  on 57  degrees of freedom
AIC: 52.392

Number of Fisher Scoring iterations: 5

bb.fit2 <- glm(basket ~ distance, family = binomial, data = bb.df)
summary(bb.fit2)

Call:
glm(formula = basket ~ distance, family = binomial, data = bb.df)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.4118  -0.4818   0.2873   0.2873   2.1029  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   5.7980     1.4038   4.130 3.63e-05 ***
distance     -2.6310     0.6274  -4.193 2.75e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 82.108  on 59  degrees of freedom
Residual deviance: 46.937  on 58  degrees of freedom
AIC: 50.937

Number of Fisher Scoring iterations: 5

coef(bb.fit2)
(Intercept)
5.79796774980361
distance
-2.63103340427345
exp(coef(bb.fit2))
100 * (1 - exp(coef(bb.fit2)))
(Intercept)
329.628990177678
distance
0.0720040145217848
(Intercept)
-32862.8990177678
distance
92.7995985478215
(bb.ci2 <- confint(bb.fit2))
100 * (1 - exp(bb.ci2))

Waiting for profiling to be done...
A matrix: 2 × 2 of type dbl
2.5 %97.5 %
(Intercept) 3.422396 9.037020
distance-4.103523-1.568945
A matrix: 2 × 2 of type dbl
2.5 %97.5 %
(Intercept)-2964.27509-840767.86136
distance 98.34856 79.17351
 
predn.df <- data.frame(distance = 1:3)
bb.logit.pred <- predict(bb.fit2, newdata = predn.df)
bb.logit.pred
1
3.16693434553016
2
0.53590094125671
3
-2.09513246301674
plogis(bb.logit.pred)
1
0.959570820970203
2
0.630858358052515
3
0.109570820976233
predict(bb.fit2, newdata = predn.df, type = "response")
1
0.959570820970203
2
0.630858358052515
3
0.109570820976233
bb.logit.predses <- predict(bb.fit2, newdata = predn.df, se.fit = TRUE)$se.fit
bb.logit.predses
# Lower and upper bounds of CIs for the log-odds
lower = bb.logit.pred - 1.96 * bb.logit.predses
upper = bb.logit.pred + 1.96 * bb.logit.predses
ci = cbind(lower, upper)
plogis(ci)
1
0.815101808705842
2
0.381297733450052
3
0.643231168633725
A matrix: 3 × 2 of type dbl
lowerupper
10.827688760.9915452
20.447335410.7830016
30.033703610.3027157
 
predictGLM(bb.fit2, newdata = data.frame(distance = 1:3), type = "link")
predictGLM(bb.fit2, newdata = data.frame(distance = 1:3), type = "response")

***Estimates and CIs are on the link scale***
A matrix: 3 × 3 of type dbl
fitlwrupr
1 3.1669343 1.5693642 4.7645045
2 0.5359009-0.2114289 1.2832308
3-2.0951325-3.3558424-0.8344225
 
***Estimates and CIs are on the response scale***
A matrix: 3 × 3 of type dbl
fitlwrupr
10.95957080.827692940.9915450
20.63085840.447338810.7829992
30.10957080.033704370.3027108

15.4. Modelling the response when it is binomial (grouped binary data) via glm#

# Load dplyr package to manipulate data frames
library(dplyr)
bb.grouped.df = bb.df %>%
    group_by(gender, distance) %>%
    summarize(n = n(), propn = sum(basket) / n)
# Change tibble back to a data frame
bb.grouped.df = data.frame(bb.grouped.df)
bb.grouped.df

Error in library(dplyr): there is no package called ‘dplyr’
Traceback:

1. library(dplyr)

这样转换后，虽然结果相同，但我们可以做卡方检验了（手动经历了分组）。

bb.fit3 = glm(propn ~ distance * gender,
    weights = n,
    family = binomial, data = bb.grouped.df
)
summary(bb.fit3)

Call:
glm(formula = propn ~ distance * gender, family = binomial, data = bb.grouped.df, 
    weights = n)

Deviance Residuals: 
      1        2        3        4        5        6  
 0.9063  -0.5354   0.3367   0.8612  -0.4629   0.4376  

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)   
(Intercept)        5.5878     1.9050   2.933  0.00335 **
distance          -2.4159     0.8181  -2.953  0.00314 **
genderM            0.6710     2.9236   0.230  0.81848   
distance:genderM  -0.5668     1.3214  -0.429  0.66795   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 38.2749  on 5  degrees of freedom
Residual deviance:  2.3688  on 2  degrees of freedom
AIC: 20.23

Number of Fisher Scoring iterations: 4

1 - pchisq(2.3688, 2)
0.305929682251732
plot(bb.fit3, which = 1, lty = 2)
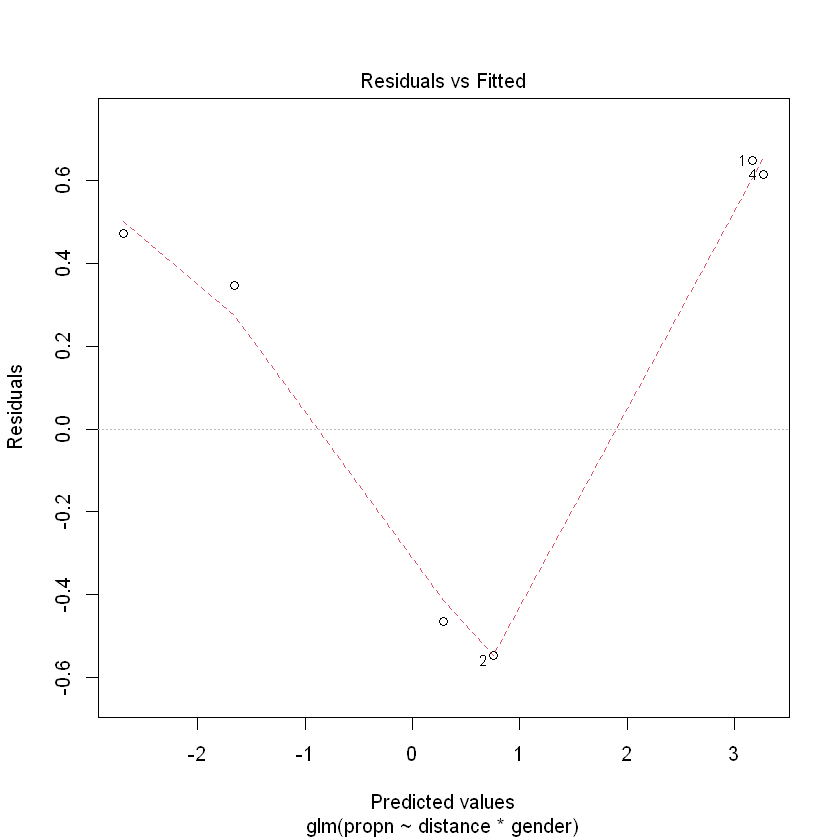
_images/819be324a0af37d61263b3baddc77190c889aef66e7fefb8578ab9f6aa588114.png 
bb.grouped.df <- transform(bb.grouped.df, success = n * propn, fail = n * (1 - propn))
bb.grouped.df
A data.frame: 6 × 6
genderdistancenpropnsuccessfail
<chr><int><int><dbl><dbl><dbl>
F1101.0100
F2100.6 64
F3100.2 28
M1101.0100
M2100.5 55
M3100.1 19
 
bb.fit4 = glm(cbind(success, fail) ~ distance * gender,
    family = binomial,
    data = bb.grouped.df
)
summary(bb.fit4)

15.5. Example 1: Space shuttle Challenger accident#

The NASA space shuttle Challenger broke up during launch on the cold morning of 28 January 1986. Most of the crew survived the initial break-up, but are believed to have been killed when the crew capsule hit the ocean at high speed. 1986年1月28日的寒冷早晨，美国宇航局的挑战者号航天飞机在发射过程中解体。大多数机组人员在最初的解体过程中幸存下来，但据信在机组人员舱高速撞向海洋时被杀死。

Space.df <- read.table("../data/ChallengerShuttle.txt", head = TRUE)
Space.df$Temp
Space.df$Failure
  1. 66
  2. 70
  3. 69
  4. 68
  5. 67
  6. 72
  7. 73
  8. 70
  9. 57
  10. 63
  11. 70
  12. 78
  13. 67
  14. 53
  15. 67
  16. 75
  17. 70
  18. 81
  19. 76
  20. 79
  21. 75
  22. 76
  23. 58
  1. 0
  2. 1
  3. 0
  4. 0
  5. 0
  6. 0
  7. 0
  8. 0
  9. 1
  10. 1
  11. 1
  12. 0
  13. 0
  14. 2
  15. 0
  16. 0
  17. 0
  18. 0
  19. 0
  20. 0
  21. 2
  22. 0
  23. 1
Space.gfit = glm(cbind(Failure, 6 - Failure) ~ Temp,
    family = binomial,
    data = Space.df
)
summary(Space.gfit)

Call:
glm(formula = cbind(Failure, 6 - Failure) ~ Temp, family = binomial, 
    data = Space.df)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-0.95227  -0.78299  -0.54117  -0.04379   2.65152  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  5.08498    3.05247   1.666   0.0957 .
Temp        -0.11560    0.04702  -2.458   0.0140 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 24.230  on 22  degrees of freedom
Residual deviance: 18.086  on 21  degrees of freedom
AIC: 35.647

Number of Fisher Scoring iterations: 5

predictGLM(Space.gfit, newdata = data.frame(Temp = 31), type = "response")

6 * predictGLM(Space.gfit, newdata = data.frame(Temp = 31), type = "response")