3. The null model

本课程前置需要装的包：

require(s20x)
require(bootstrap)

Show code cell output Hide code cell output

Loading required package: s20x

Loading required package: bootstrap

3.1. Revisiting the null model 回顾零模型

本节同样以 Stats20x 的学生考试成绩为例：

Stats20x.df <- read.table("../data/STATS20x.txt", header = TRUE, sep = "\t")

零模型就是把线性模型中的斜率去掉，或斜率指定常数，从而排除其影响单独分析截距。本节将重点讲述零模型的最大作用：T检验。

一文详解t检验 - 知乎

t检验（t test）又称学生t检验（Student t-test）可以说是统计推断中非常常见的一种检验方法，用于统计量服从正态分布，但方差未知的情况。

t检验的前提是要求样本服从正态分布或近似正态分布，不然可以利用一些变换（取对数、开根号、倒数等等）试图将其转化为服从正态分布是数据，如若还是不满足正态分布，只能利用非参数检验方法。不过当样本量大于30的时候，可以认为数据近似正态分布。

t检验最常见的四个用途：

• 单样本均值检验（One-sample t-test） 用于检验 “总体方差未知、正态数据或近似正态的” 单样本的均值，是否与已知的总体均值相等。

• 两独立样本均值检验（Independent two-sample t-test） 用于检验两对 “独立的，正态数据或近似正态的” 样本的均值是否相等，这里可根据总体方差是否相等分类讨论。

• 配对样本均值检验（Dependent t-test for paired samples） 用于检验一对配对样本的均值的差，是否等于某一个值

• 回归系数的显著性检验（t-test for regression coefficient significance） 用于检验回归模型的解释变量，对被解释变量是否有显著影响

# 建立回归模型
examtest.fit <- lm(Exam ~ Test, data = Stats20x.df)
examtest.fit2 <- lm(Exam ~ 1, data = Stats20x.df)

# 绘图
plot(Exam ~ Test, data = Stats20x.df, col = "grey")
abline(examtest.fit, col = "blue", lty = 2)
abline(examtest.fit2, col = "red", lty = 2)

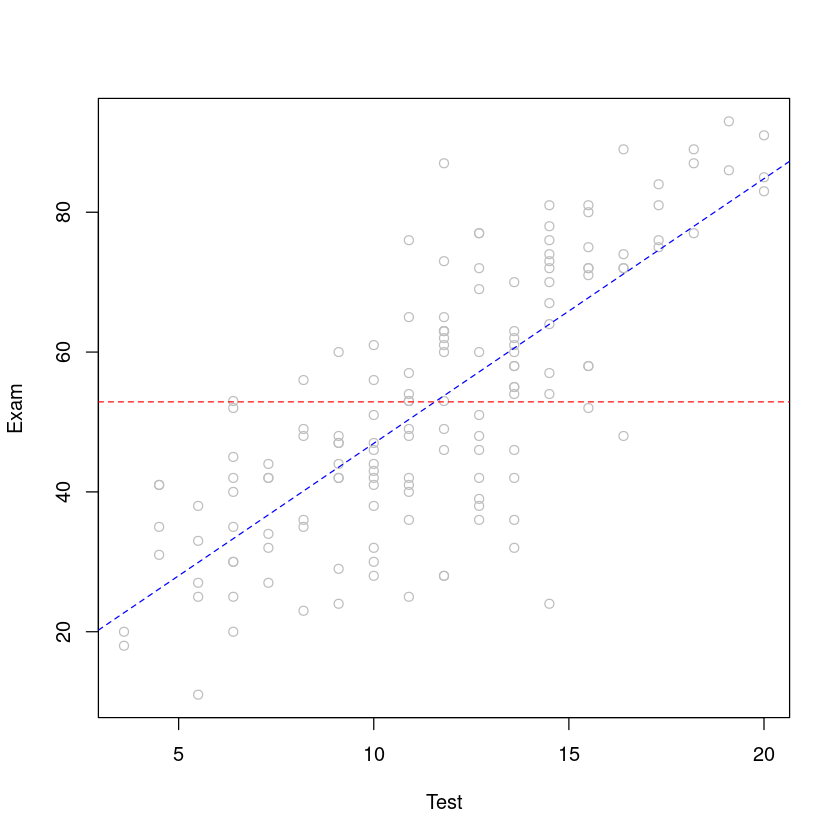
推断总体均值：

To save some typing we’ll let y be the vector Stats20x.df$Exam of exam scores.

y <- Stats20x.df$Exam
hist(y, breaks = 20, main = "") # Use main to suppress plot title

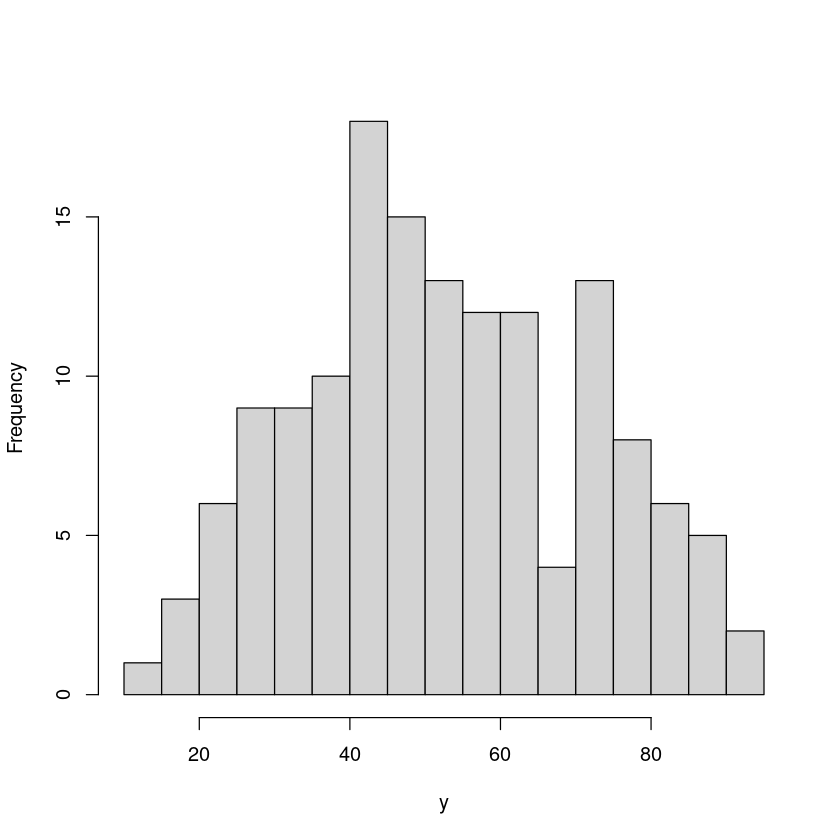
继续使用零模型做线性回归，使其更关注于y值的置信关系与p检验。

null.fit <- lm(y ~ 1)
# Only give coefficients from summary 将系数板块单独提取出做展示
coef(summary(null.fit))
# 获得该零模型的对应置信区间
confint(null.fit)

A matrix: 1 × 4 of type dbl

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	52.87671	1.545802	34.20666	2.632011e-71

A matrix: 1 × 2 of type dbl

	2.5 %	97.5 %
(Intercept)	49.8215	55.93193

Conclusion:

• The near zero \(Pr(>|t|)\) p-value totally rejects(拒绝) the null hypothesis(零假设) that \(H0 : µ ≡ β0 = 0\).

• The 95% confidence interval(置信区间) for \(µ\) is 49.82 to 55.93.

3.2. Revisiting the t-test

\[ T = \frac {\bar{y} - \mu} {\frac{s}{\sqrt n}} \sim t_{n-1} \]

其中 \(\bar{y}\) 为样本均值，\(s\) 为样本标准差。

\[ s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar X)^2} \]

n <- length(y) # 146 students
tstat <- (mean(y) - 0) / (sd(y) / sqrt(n))
tstat

34.2066579217089

## t-multiplier
tmult <- qt(1 - .05 / 2, df = n - 1)
## We want the upper 97.5% (or 1-.05/2) bound of the CI
## NOTE: mean = sample mean; sd = standard deviation; sqrt = square root
mean(y) - tmult * sd(y) / sqrt(n)

## Upper bound of CI 置信区间上限
mean(y) + tmult * sd(y) / sqrt(n)
## Or if we want both the lower and upper bounds of the CI in one statement
## 置信区间下限
mean(y) + c(-1, 1) * tmult * sd(y) / sqrt(n)

49.8214976403875

55.9319270171467

1. 49.8214976403875
2. 55.9319270171467

零模型就是单样本T检验。

手动随机抽样检验我们的结果：

## Resampling the exam marks, N times with replacement:
N <- 10000 # The number of bootstrap resamples we want
# The new sample means are stored in ybar
ybar <- rep(NA, N) ## A vector of length N to store our resampled means

## A loop - allows us to do something N (10,000) times
for (i in 1:N) {
    ## Take the average of this sample (below) from a sample of size n = 146 from y - with replacement
    ybar[i] <- mean(sample(y, n, replace = T))
}
mean(ybar)

52.8874787671233

library(bootstrap)
ybar <- bootstrap(Stats20x.df$Exam, 10000, mean)$thetastar
mean(ybar)

52.8795863013699

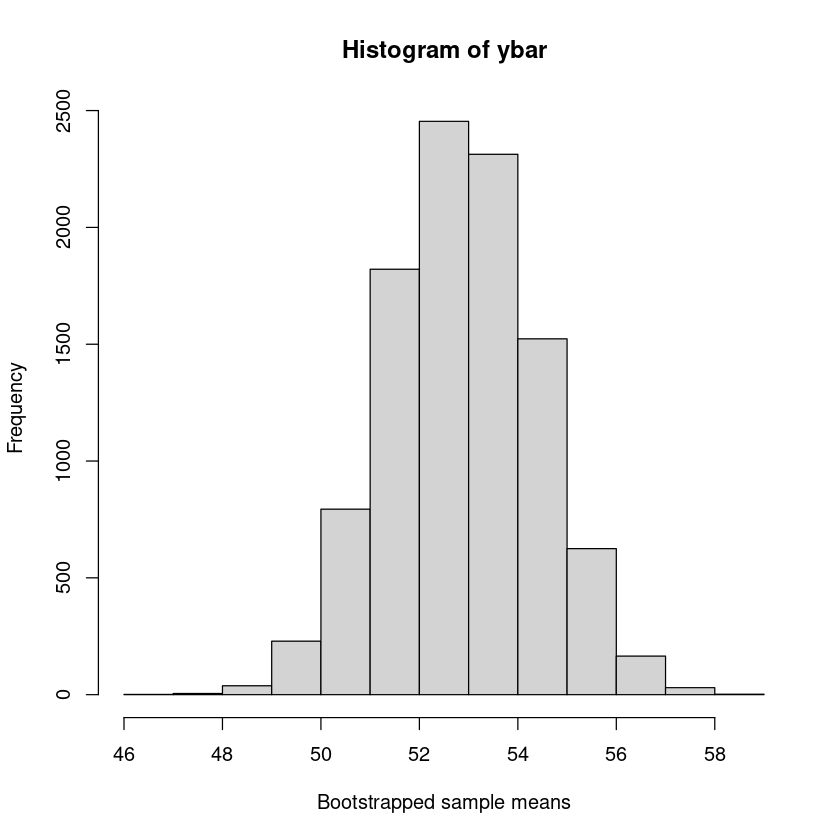
## Histogram of these 10,000 bootstrap means
hist(ybar, xlab = "Bootstrapped sample means")

3.3. The paired t-test

For a meaningful comparison, We will need to make them have the same scale, so we multiply the test mark by 5 so that it is also out of 100.

Stats20x.df$Test2 <- 5 * Stats20x.df$Test
## Check that it worked
Stats20x.df[1:3, c("Exam", "Test", "Test2")]

A data.frame: 3 × 3

	Exam	Test	Test2
	<int>	<dbl>	<dbl>
1	42	9.1	45.5
2	58	13.6	68.0
3	81	14.5	72.5

Stats20x.df$Diff <- Stats20x.df$Test2 - Stats20x.df$Exam
## Check the first 5 measurements
Stats20x.df[1:5, c("Test2", "Exam", "Diff")]

A data.frame: 5 × 3

	Test2	Exam	Diff
	<dbl>	<int>	<dbl>
1	45.5	42	3.5
2	68.0	58	10.0
3	72.5	81	-8.5
4	95.5	86	9.5
5	41.0	35	6.0

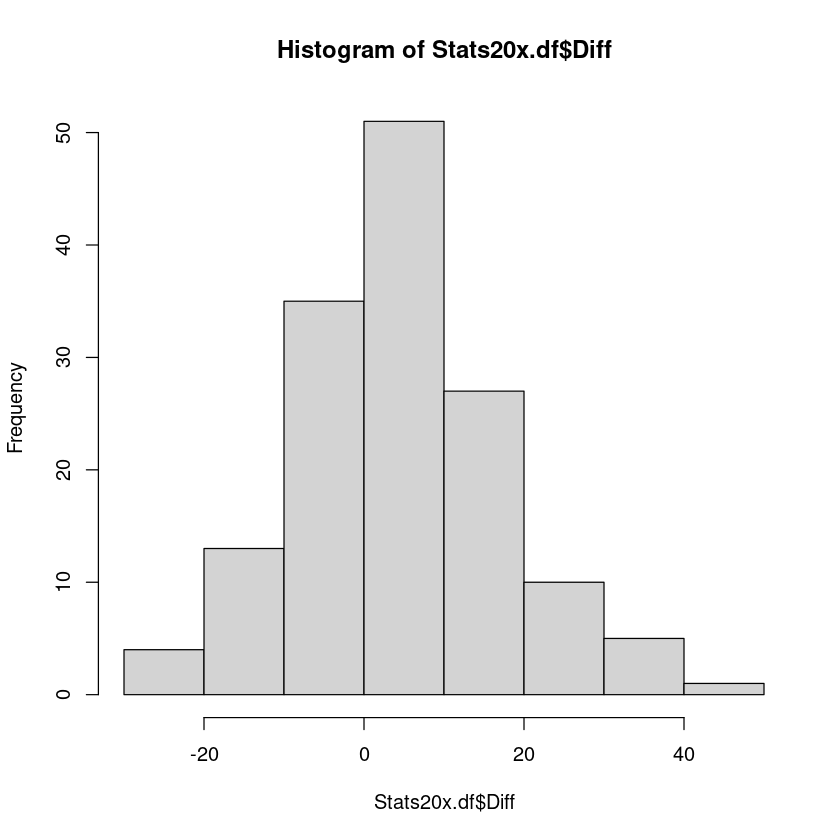
hist(Stats20x.df$Diff)