5. Linear models with a categorical (factor) explanatory variable

本节需要的包：

require(s20x)

Show code cell output Hide code cell output

Loading required package: s20x

5.1. Using categorical variables as explanatory variables by using indicator variables

使用指标变量将分类变量用作解释变量

library(s20x)
## Importing data into R
Stats20x.df <- read.table("../data/STATS20x.txt", header = T)
## Change Attend from a character variable to a factor variable
Stats20x.df$Attend <- as.factor(Stats20x.df$Attend)
## Examine the data
Stats20x.df$Attend[1:20]

1. Yes
2. Yes
3. Yes
4. Yes
5. No
6. Yes
7. Yes
8. No
9. Yes
10. Yes
11. No
12. Yes
13. No
14. No
15. No
16. Yes
17. Yes
18. No
19. Yes
20. Yes

Levels:

1. 'No'
2. 'Yes'

简要分析数据集，确保有你需要的可能的关系：

summaryStats(Stats20x.df$Exam, Stats20x.df$Attend)
plot(Exam ~ Attend, data = Stats20x.df)

    Sample Size     Mean Median  Std Dev Midspread
No           46 42.21739   40.5 16.34206     20.50
Yes         100 57.78000   58.0 17.67757     28.25

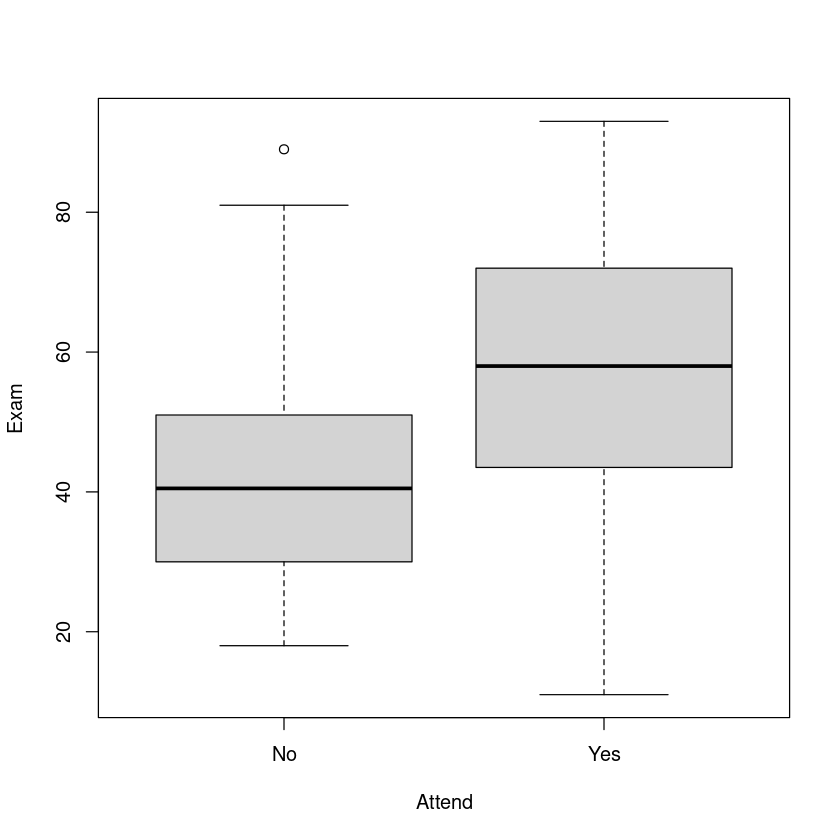
缺勤的确会让学生成绩变低，在数据分布上的确有一定的关系。

为了在后面进行更好的分析，我们将缺勤的 Yes 和 No 转换为 1 和 0：

# Make a new variable Attend2 which is 1 if Attend = "Yes" and 0 otherwise

# Note how we use two equal signs, ==, to test equality
Stats20x.df$Attend2 <- as.numeric(Stats20x.df$Attend == "Yes")
with(Stats20x.df, table(Attend, Attend2))

      Attend2
Attend   0   1
   No   46   0
   Yes   0 100

trendscatter(Exam ~ Attend2, data = Stats20x.df)

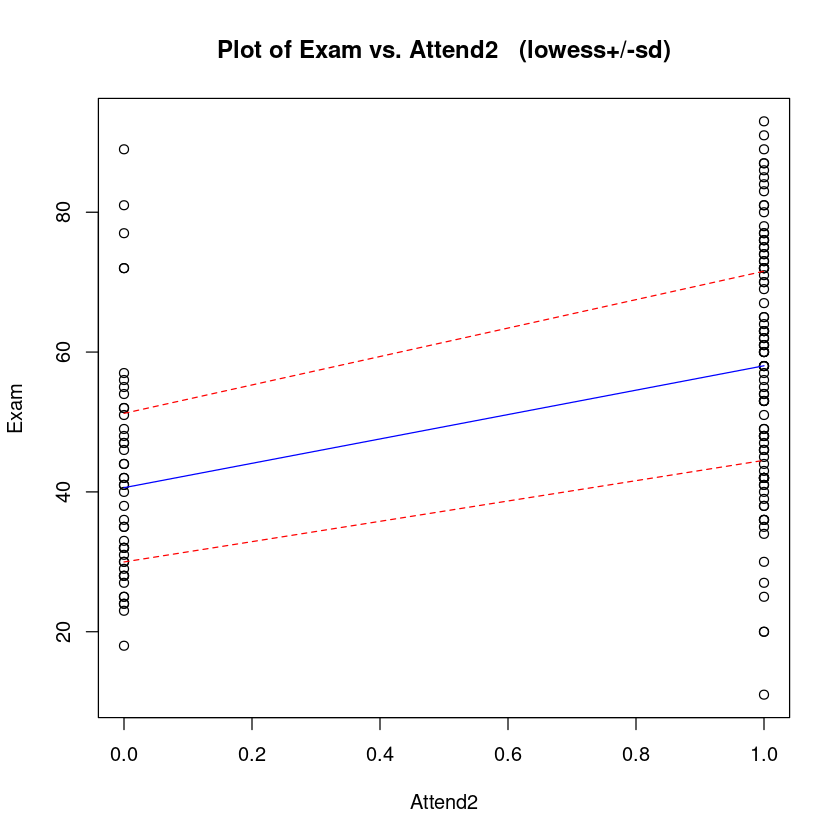
The linear model for the expected value of is

\[ E[Exam|Attend2] = \beta_0 + \beta_1 Attend2 \]

其中 \(\beta_0\) 是截距，即所有缺勤的均值；\(\beta_1\) 是考试成绩和缺勤的关系，由缺勤和出勤的成绩关系共同决定。

examattend2.fit <- lm(Exam ~ Attend2, data = Stats20x.df)
summary(examattend2.fit)

Call:
lm(formula = Exam ~ Attend2, data = Stats20x.df)

Residuals:
    Min      1Q  Median      3Q     Max 
-46.780 -13.108  -0.217  12.642  46.783 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   42.217      2.547  16.578  < 2e-16 ***
Attend2       15.563      3.077   5.058 1.27e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 17.27 on 144 degrees of freedom
Multiple R-squared:  0.1508,	Adjusted R-squared:  0.145 
F-statistic: 25.58 on 1 and 144 DF,  p-value: 1.271e-06

上述拟合代表 x 为 Attend2（0 和 1） 时，y 的期望值，即考试成绩的期望值。

但注意事实上，直接使用 lm() 函数进行拟合，也能得出正确的结果，因为 lm() 函数会自动将分类变量转换为指标变量（AttendYes）：

examattend.fit <- lm(Exam ~ Attend, data = Stats20x.df)
summary(examattend.fit)

Call:
lm(formula = Exam ~ Attend, data = Stats20x.df)

Residuals:
    Min      1Q  Median      3Q     Max 
-46.780 -13.108  -0.217  12.642  46.783 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   42.217      2.547  16.578  < 2e-16 ***
AttendYes     15.563      3.077   5.058 1.27e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 17.27 on 144 degrees of freedom
Multiple R-squared:  0.1508,	Adjusted R-squared:  0.145 
F-statistic: 25.58 on 1 and 144 DF,  p-value: 1.271e-06

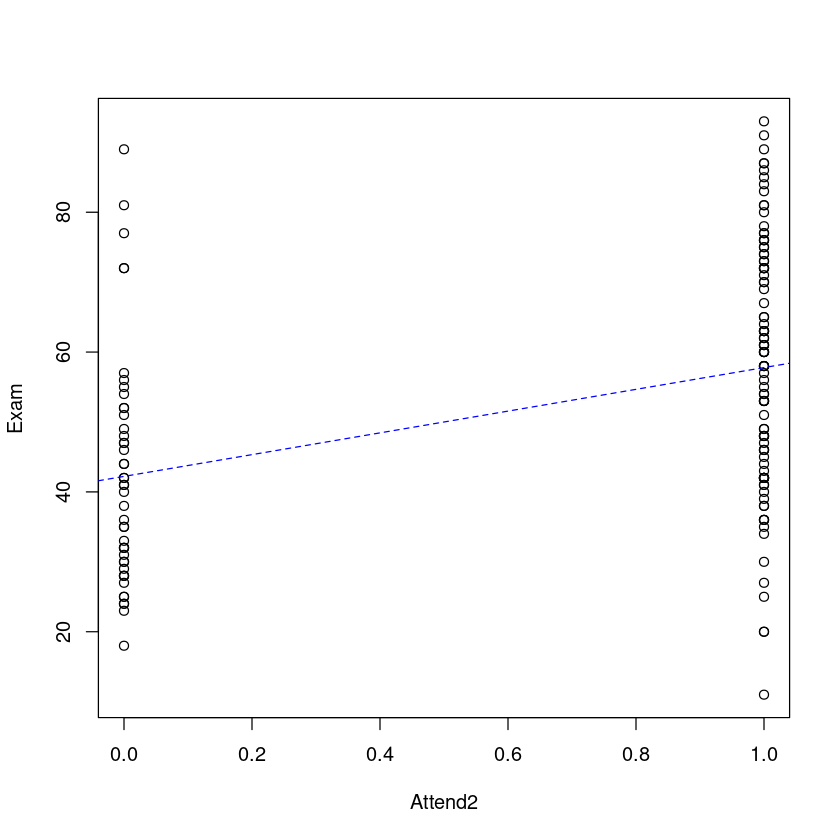
让我们将拟合模型可视化。在这里，我们将使用虚拟变量拟合我们的模型得到的"最佳"估计直线绘制出来。

plot(Exam ~ Attend2, data = Stats20x.df)
## Add the lm estimated line to this plot where a=intercept, b=slope
abline(coef(examattend.fit), lty = 2, col = "blue")

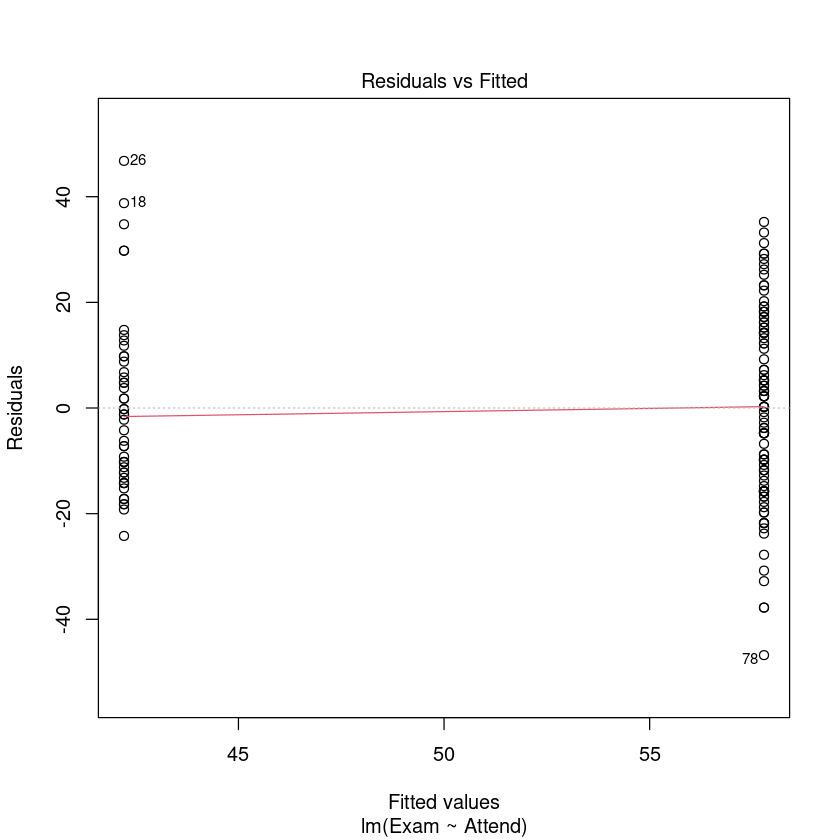
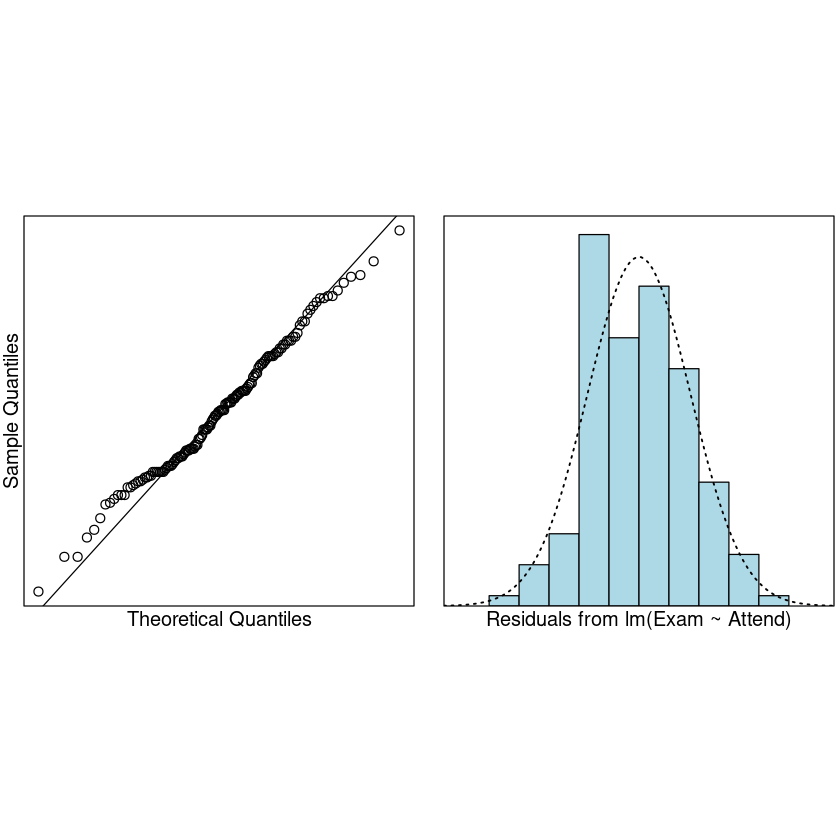
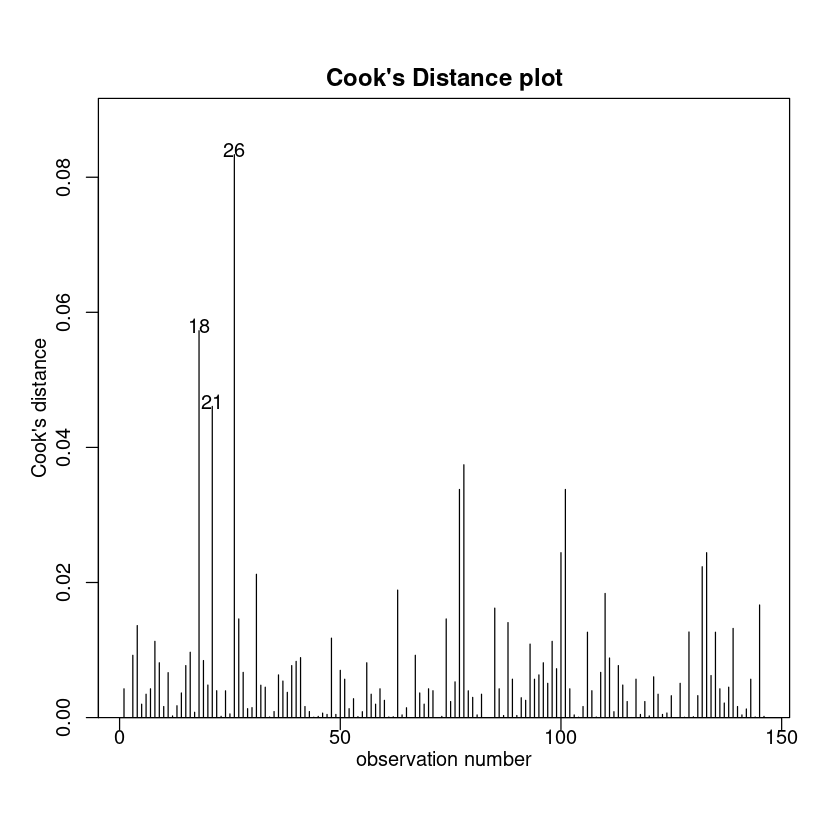
模型建立好了，接下来就是我们经典的模型检验三步走了：

1. 残差均值接近于 0

2. 残差满足正态分布

3. 没有或排除了异常点

plot(examattend.fit, which = 1)
normcheck(examattend.fit)
cooks20x(examattend.fit)

## Create data frame of values of interest: Attend=="Yes" and "No"
## Make sure that the names of vars are exactly the same as in the data frame
preds.df <- data.frame(Attend = c("No", "Yes"))
predict(examattend.fit, preds.df, interval = "confidence")
predict(examattend.fit, preds.df, interval = "prediction")

A matrix: 2 × 3 of type dbl

	fit	lwr	upr
1	42.21739	37.18401	47.25077
2	57.78000	54.36619	61.19381

A matrix: 2 × 3 of type dbl

	fit	lwr	upr
1	42.21739	7.710259	76.72452
2	57.78000	23.471673	92.08833

再次强调：“confidence”是代表均值预测范围，而“prediction”是代表个体预测范围。