04 数值的机器运算 (4~6)
定点乘法运算
在计算机中,乘法运算大多数由累加与移位来实现,也有些机器中具有由大规模集成电路制造的阵列乘法模块。
原码一位乘法
原码一位乘法算法
原码一位乘法是从手算演变而来的,即用两个操作数的绝对值相乘,乘积的符号为两操作数符号的异或值(同号为正,异号为负)。即:
- 乘积:
- 符:
式中:为乘积的符号,和为被乘数和乘数的符号。

原码一位乘法的规则:
- 参加运算的操作数取其绝对值;
- 令乘数的最低位为判断位,若为“1”,加被乘数,若为“0”,不加被乘数(加 0);
- 累加后的部分积以及乘数右移一位;
- 重复 n 次 ⑵ 和 ⑶ ;
- 符号位单独处理,同号为正,异号为负。

通常,乘法运算需要 3 个寄存器。
- 被乘数存放在 B 寄存器中;
- 乘数存放在 C 寄存器中;A 寄存器用来存放部分积与最后乘积的高位部分,它的初值为 0。
- 运算结束后寄存器 C 中不再保留乘数,改为存放乘积的低位部分。
原码一位乘法流程图:
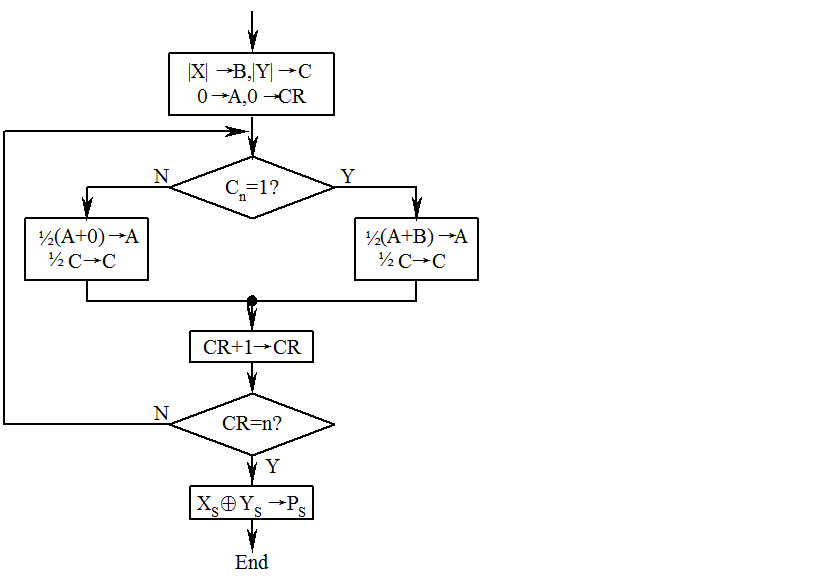
原码一位乘法运算的实现
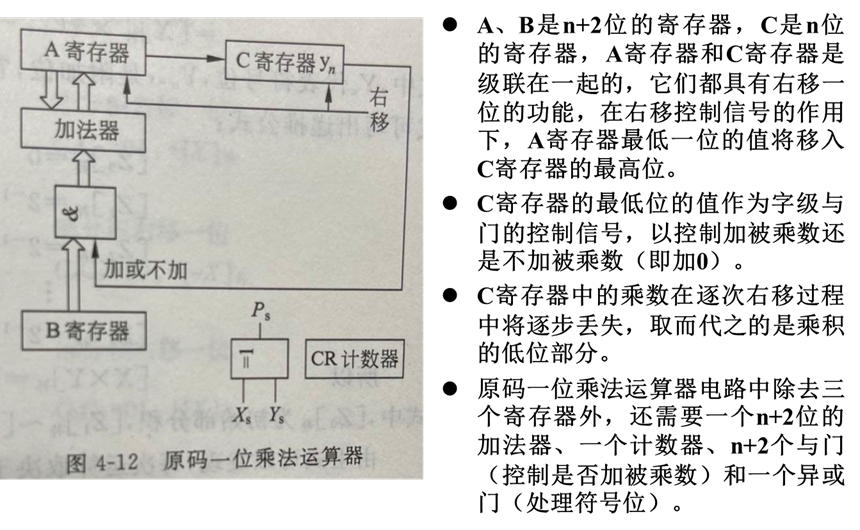
补码一位乘法
虽然原码乘法比补码乘法容易实现,但因为补码加减法简单,在以加减运算为主的通用机中操作数都用补码表示,所以这类计算机在做乘法时常使用补码乘法。
校正法
校正法是将[X]补和[Y]补按原码规则运算,所得结果根据情况再加以校正,从而得到正确的[X×Y]补。补码乘法的统一表达式:
比较法——Booth 乘法
递推公式:

Booth 乘法规则:
- 参加运算的数用补码表示;
- 符号位参加运算;
- 乘数最低位后面增加一位附加位,其初值为 0;
- 由于每求一次部分积要右移一位,所以乘数的最低两位、的值决定了每次应执行的操作;
- 移位按补码右移规则进行;
- 共需做 n+1 次累加,n 次移位,第 n+1 次不移位。
Booth 乘法运算操作:

由于符号位要参加运算,部分积累加时最高有效位产生的进位可能会侵占符号位,故被乘数和部分积应取双符号位,而乘数只需要一位符号位。运算时仍需要有 3 个寄存器,各自的作用与原码时相同,只不过存放的内容均为补码表示而已。
Booth 乘法流程图:
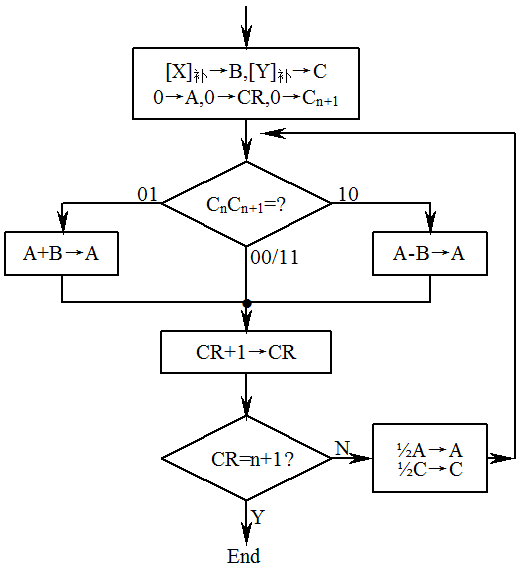
Booth 乘法运算的实现
各器件的作用与原码一位乘法相同,A、B 寄存器长 n+2 位,C 寄存器长 n+1 位,还需一个 n+2 位的加法器、n+2 个与或门和一个计数器。由 C 寄存器的最低两位 CnCn+1 来控制是加/减被乘数还是加 0,当 CnCn+1=01 时,加被乘数,即加 B 寄存器的内容;CnCn+1=10 时,减被乘数,即加上 B 寄存器中内容的反,并在加法器的最低位加 1;CnCn+1=00 或 11 时,不加也不减(加 0)。由于符号位参与运算,所以不需要专门处理符号位的异或门。
补码两位乘法
为了提高乘法的执行速度,可以选用两位乘法的方案。所谓两位乘法,就是每次处理乘数中的两位,从而使乘法的速度提高了一倍。
根据 Booth 乘法方便地推导出补码两位乘法,即把补码两位乘理解为将 Booth 乘法的两次合并为一次来做。
补码两位乘法操作:

被乘数和部分积取 3 符号位,当乘数的数值位 n 为偶数时,乘数取两符号位,共需作 n/2 +1 次累加,n/2 次移位(最后一次不移位);当 n 为奇数时,乘数只需一个符号位,共需 (n+1)/2 次累加和移位,但最后一次仅移一位。
例 10:已知:X=0.0110011,Y=-0.0110010,求:X×Y。
[X]补=000.0110011→B,
[Y]补=1.1001110→C,0→A
2[X]补=000.1100110,
[-X]补=111.1001101,2[-X]补=111.0011010
补码两位乘法示例:

定点除法运算
除法是乘法的逆运算,与乘法运算的处理思想相似,可以将 n 位除转化成若干次“减法-移位”,也有些计算机具有由大规模集成电路制造的阵列除法模块。
原码除法运算

原码比较法和恢复余数法
比较法
比较法类似于手工运算,只是为了便于机器操作,将除数右移改为部分余数左移,每一位的上商直接写到寄存器的最低位。l 设 A 寄存器中存放被除数(或部分余数),B 寄存器中存放除数,C 寄存器用来存放商 Q,l 若 A≥B,则上商 1,并减除数;l 若 A<B,则上商 0。比较法需要设置比较线路,从而增加了硬件的代价。
比较过程的流程图:
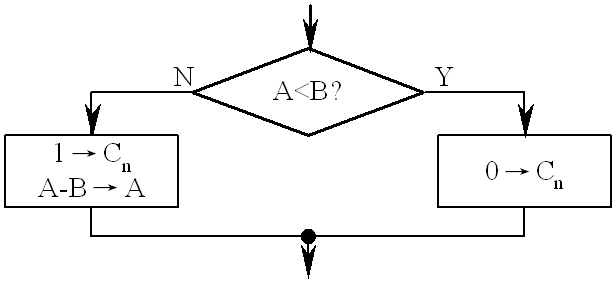
恢复余数法
- 恢复余数法是直接作减法试探方法,不管被除数(或部分余数)减除数是否够减,都一律先做减法。
- 若部分余数为正,表示够减,该位商上“1”;
- 若部分余数为负,表示不够减,该位商上“0”,并要恢复余数。 恢复余数过程的流程图
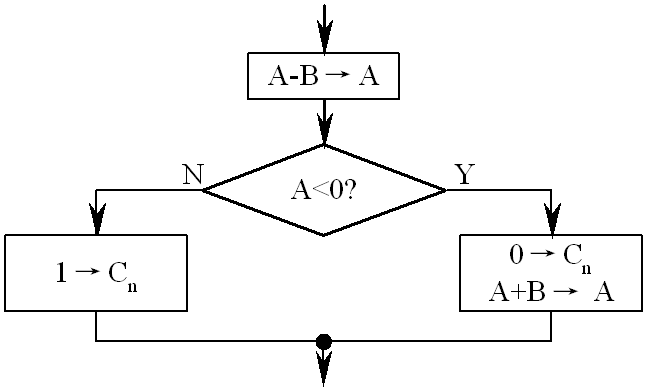
- 由于部分余数的正、负是根据不同的操作数组合随机出现的,恢复除数法会使得除法运算的实际操作次数不固定,从而导致控制电路比较复杂。
- 而且在恢复余数时,要多作一次加法,降低了除法的执行速度。
- 因此,原码恢复余数法在计算机中一般很少采用。
原码不恢复余数法(原码加减交替法)
原码不恢复余数法是对恢复余数法的一种改进,它减少了浪费的加法时间,且运算的次数固定,故被广泛采用。l 在恢复余数法中,若第 i-1 次求商的部分余数为 ri-1,则第 i 次求商操作为:,
若够减,部分余数,商 1。
若不够减,部分余数,商 0,恢复余数后,,然后再左移一位,进行第次操作:
原码不恢复余数除法由下面的通式表示:
式中 Qi 为第 i 次所得的商,若部分余数为正,则 Qi=1,部分余数左移一位,下一次继续减除数;若部分余数为负,则 Qi=0,部分余数左移一位,下一次加除数。由于加减运算交替地进行,故称为原码加减交替法。
例 12:已知:X=-0.10101,Y=0.11110,求:X÷Y。
|X|=00.10101→A,|Y|=00.11110→B,0→C
[|Y|]变补=11.00010
原码不恢复余数除法示例:
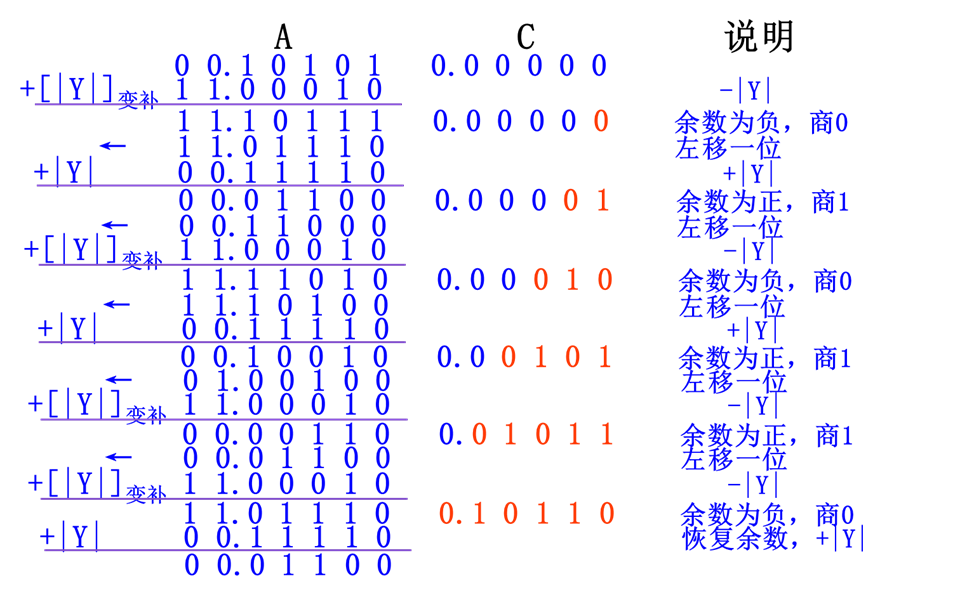
经过原码不恢复余数除法,有: 商= 余数=
除法运算需要 3 个寄存器。A 和 B 寄存器分别用来存放被除数和除数,C 寄存器用来存放商,它的初值为 0。运算过程中 A 寄存器的内容为部分余数,它将不断地变化,最后剩下的是扩大了若干倍的余数,只有将它乘上 2-n 才是真正的余数。
原码加减交替除法流程图:
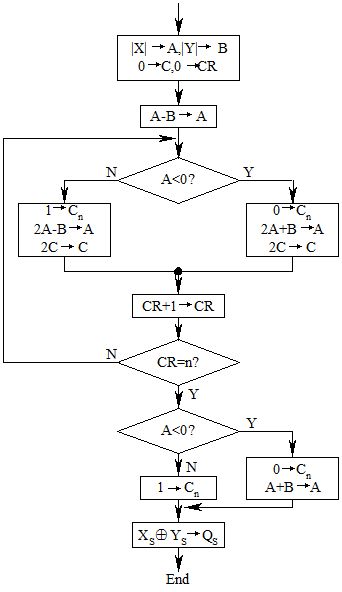
- 在定点除法运算时,为了防止溢出,要求被除数的绝对值小于除数的绝对值,(除外),且除数不能为 0。
- 因此第一次减除数肯定是不够减的,如果我们采用先移位后减除数的方法,得到的结果也是相同的。
- 另外,在原码加减交替法中,当最终余数为负数时,必须恢复一次余数,使之变为正余数,注意此时不需要再左移了。
原码加减交替除法的实现
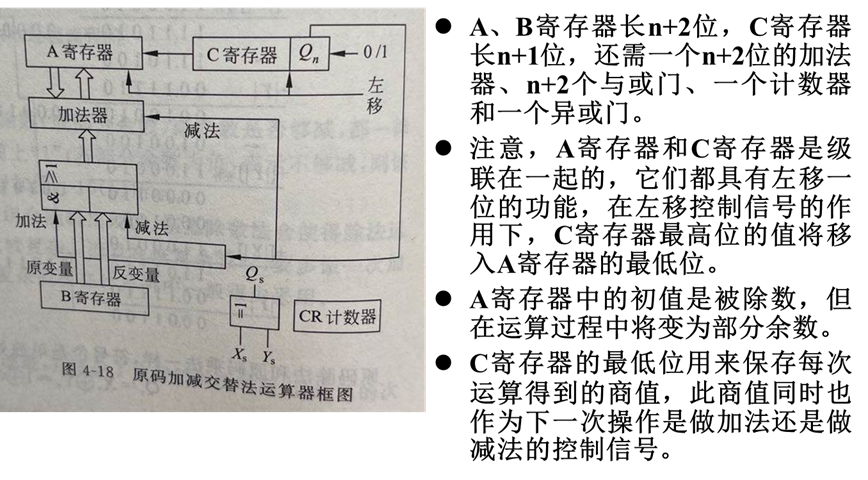
补码除法运算
够减的判断
参加运算的两个数符号任意,当被除数(或部分余数)的绝对值大于或等于除数的绝对值时,称为够减;反之称为不够减。当两数同号时,实际应作减法;两数异号时,实际应作加法。
判断的方法和结果如下:当被除数(或部分余数)与除数同号时,如果得到的新部分余数与除数同号,表示够减,否则为不够减;当被除数(或部分余数)与除数异号时,如果得到的新部分余数与除数异号,表示够减,否则为不够减。
上商规则
补码除法运算的商也是用补码表示的,上商的规则是:如果[X]补和[Y]补同号,则商为正数,够减时上商“1”,不够减时上商“0”;如果[X]补和[Y]补异号,则商为负数,够减时上商“0”,不够减时上商“1”。
补码的上商规则可归结为:
部分余数[ri]补和除数[Y]补同号,商上“1”,反之,商上“0”。
商符的确定
商符是在求商的过程中自动形成的,按补码上商规则,第一次得出的商,就是实际应得的商符。为了防止溢出,必须有|X|<|Y|,所以第一次肯定不够减。当被除数与除数同号时,部分余数与除数必然异号,商上“0”,恰好与商符一致;当被除数与除数异号,部分余数与除数必然同号,商上“1”,也恰好就是商的符号。
求新部分余数
求新部分余数[ri+1]补的通式如下:
[ri+1]补=2[ri]补+(1-2Qi)×[Y]补
Qi 表示第 i 步的商。若商上“1”,下一步操作为部分余数左移一位,减去除数;若商上“0”,下一步操作为部分余数左移一位,加上除数。
末位恒置 1
商的最末一位恒置为“1”,运算的最大误差为 2-n。此法操作简单,易于实现。
补码加减交替除法规则
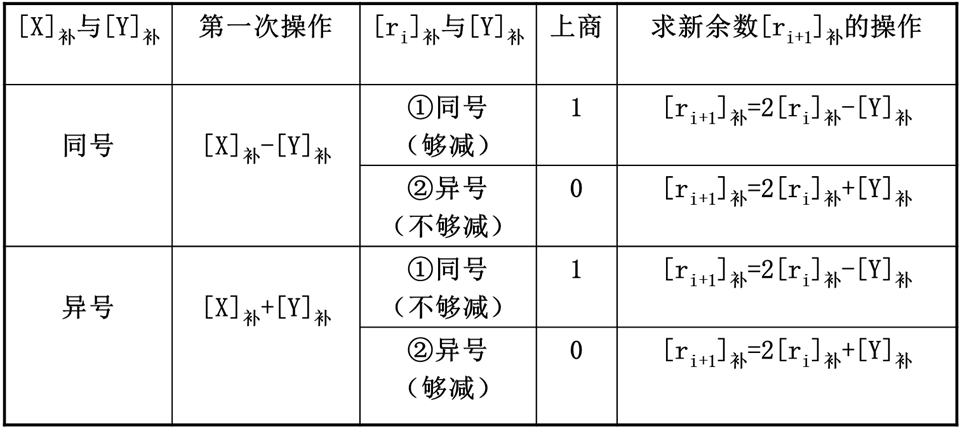
补码加减交替除法示例
例 13:已知 X=0.1000,Y=-0.1010;求 X÷Y。
[X]补=00.1000→A,
[Y]补=11.0110→B,0→C
[-Y]补=00.1010


补码加减交替除法流程图

图 4-19 补码加减交替除法流程图
规格化浮点运算
浮点加减运算
第 2 章中已经讨论了浮点数的表示方法,这里将进一步讨论规格化浮点数的四则运算问题,其中尾数的基值 r=2。
设两个非 0 的规格化浮点数分别为:
规格化浮点数 A、B 加减运算通式为:
浮点数加减运算步骤
对阶
两个浮点数相加或相减,首先要把小数点的位置对齐,而浮点数的小数点的实际位置取决于阶码的大小,因此,对齐两数的小数点,就是使两数的阶码相等,这个过程称为对阶。
要对阶,首先应求出两数阶码 EA 和 EB 之差
- 若 ΔE=0,表示两数阶码相等,即;
- 若 ΔE > 0,表示 EA > EB;
- 若 ΔE < 0,表示 EA < EB。 当 EA≠EB 时,要通过尾数的移位来改变 EA 或 EB。对阶的规则是:小阶向大阶看齐。要使小阶的阶码增大,则相应的尾数右移,直到两数的阶码相等为止。每右移一位,阶码加 1。
- EA > EB,则 MB 右移。每右移一位,,直至 EA=EB 为止。
- EA < EB,则 MA 右移。每右移一位,,直至 EA=EB 为止。l 尾数右移后,应对尾数进行舍入。
尾数加/减
对阶之后,就可以进行尾数加/减,即:
其算法与定点加/减法相同。
尾数结果规格化
尾数加/减运算之后得到的数可能不是规格化数,为了增加有效数字的位数,提高运算精度,必须进行结果规格化操作。
尾数结果规格化:
设尾数用双符号位补码表示,经过加/减运算之后,可能出现以下 6 种情况,即:
① 00.1 xx…x
② 11.0 x x…x
③ 00.0 x x…x
④ 11.1 x x…x
⑤ 01.x x x…x
⑥ 10.x x x…x
第 ① 和 ② 种情况,已是规格化数。
第 ③ 和 ④ 种情况需要使尾数左移以实现规格化,这个过程称为左规。尾数每左移一位,阶码相应减 1(),直至成为规格化数为止。
左规可以进行多次。式中 Cs1、Cs2 表示尾数 MC 的两个符号位,C1 为 MC 的最高数值位。
第 ⑤ 和 ⑥ 种情况在在定点加减运算中称为溢出;但浮点加减运算中,只表明此时尾数的绝对值大于 1,而并非真正的溢出。这种情况应将尾数右移以实现规格化。这个过程称为右规。尾数每右移一位,阶码相应加 1()。
右规最多只有一次。
舍入
最简单的舍入方法是恒舍法,即无条件的丢掉正常尾数最低位之后的全部数值。
溢出判断
当尾数右规后,根据阶码来判断浮点运算结果是否溢出。
,表示上溢。此时,浮点数真正溢出,机器需停止运算,做溢出中断处理。
,表示下溢。浮点数值趋于零,机器不做溢出处理,而是按机器零处理。
浮点数加减运算举例
有两浮点数为
假设这两数的格式:阶码 4 位,用移码(偏置值为)表示;尾数 8 位,用补码表示,包含一位符号位,即
阶码 尾数
[A]浮=0111;0.1011100
[B]浮=0110;1.0101010
对阶
求阶差:
ΔE=1,表示 EA > EB。按对阶规则,将 MB 右移一位,EB+1→EB,得:
尾数求和
尾数结果规格化
由于结果的尾数是非规格化的数,故应左规。尾数每左移一位,阶码减 1,直至尾数成为规格化数为止。最后结果为
[A+B]浮=0110;0.110001
即
未发生溢出
浮点乘除运算
设两个非 0 的规格化浮点数分别为
规格化浮点数 A、B 乘除运算通式为:
乘法步骤
两浮点数相乘,其乘积的阶码应为相乘两数的阶码之和,其乘积的尾数应为相乘两数的尾数之积。即:
阶码相加
两个浮点数的阶码相加,如果阶码用补码表示,无须校正;当阶码用偏置值为 2n 的移码表示时,阶码相加后要减去一个偏移量 2n。
尾数相乘
若 MA、MB 都不为 0,则可进行尾数乘法,算法与定点数乘法算法相同。
尾数结果规格化
由于 A、B 均是规格化数,所以尾数相乘后的结果一定落在下列范围内:
当时,乘积已是规格化数,无须再进行规格化操作;当 时,则需要左规一次。左规时调整阶码后如果发生阶码下溢,则做机器零处理。
除法步骤
两浮点数相除,其商的阶码应为相除两数的阶码之差,其商的尾数应为相除两数的尾数之商。即:
尾数调整
为了保证商的尾数是一个定点小数,首先需要检测。如果不小于,则 MA 右移一位,,称为尾数调整。因为 A、B 都是规格化数,所以最多调整一次。
阶码相减
两浮点数的阶码相减,如果阶码用补码表示,阶码相减之后无须校正;当阶码用偏置值为 2n 的移码表示时,阶码相减后要加上一个偏移量 2n。阶码相减后,如有溢出,应另作处理。
尾数相除
若 MA、MB 都不为 0,则可进行尾数除法。尾数除法的算法与前述定点数除法算法相同。因为开始时已进行了尾数调整,所以运算结果一定落在规格化范围内,即
浮点运算器的实现
浮点运算的阶码只有加减运算,尾数则有加、减、乘、除四种运算。可见浮点运算器主要由两个定点运算部件组成,一个是阶码运算部件,用来完成阶码加、减,以及控制对阶时小阶的尾数右移次数和规格化时对阶码的调整;另一个是尾数运算部件,用来完成尾数的四则运算以及判断尾数是否已规格化。此外,还需要有溢出判断电路等。
现代计算机可把浮点运算部件做成任选件,或称为协处理器。所谓协处理器是因为它只能协助主处理器工作,不能单独工作。